Understanding the largest scientific experiment ever:

The large hadron collider (LHC)

Where is the LHC?

The Large Hadron Collider (LHC)  is located in a circular tunnel 27 km (17 miles) in circumference.

The tunnel is buried around 100 m (about the size of a football field) underground.

It straddles the Swiss and French borders on the outskirts of Geneva at the CERN headquarters.

Why Large, Hadron, Collider?

Large due to its size (approximately 27 km in circumference)

Hadron because it accelerates protons or ions, which are hadrons.

Collider because these particles form two beams travelling in opposite directions, which collide at four points where the two rings of the machine intersect.

What is a Particle Accelerator?

A particle accelerator is a machine that accelerates elementary particles, such as electrons or protons, to very high energies.

There are two basic types of particle accelerators: linear accelerators and circular accelerators.

Linear accelerators propel particles along a linear, or straight, beam line.

Circular accelerators propel particles around a circular track. 

The Structure of The LHC

  The beams travel in opposite directions in separate beam pipes – two tubes kept at ultrahigh vacuum.

  They are guided around the accelerator ring by a strong magnetic field maintained by superconducting electromagnets

  This requires chilling the magnets to ‑271.3°C – a temperature colder than outer space.

  For this reason, much of the accelerator is connected to a distribution system of liquid helium, which cools the magnets, as well as to other supply services.

Synchrotrons are the highest-energy particle accelerators in the world. The Large Hadron Collider currently tops the list, with the ability to accelerate particles to an energy of 6.5 trillion electronvolts before colliding them with particles of an equal energy traveling in the opposite direction.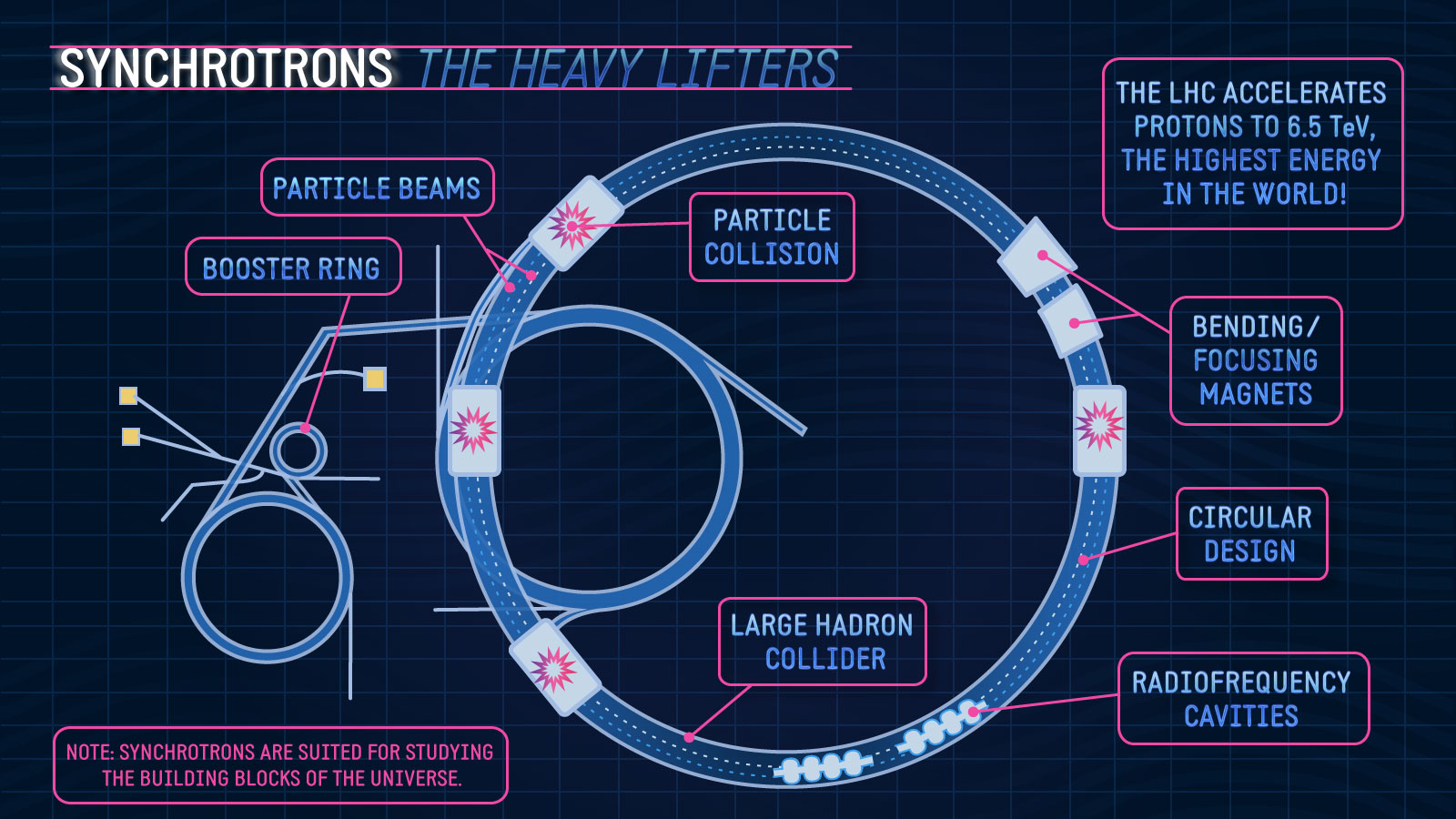 

Understanding one of the shortest papers ever in Mathematics

John Conway and Alexander Soifer submitted a paper in 2005 with the goal to write the shortest math paper ever.

It is only two words long and contains two distinct proofs of their problem in two figures.

The problem was: Can n²+1 unit equilateral Triangles cover an equilateral triangle of side >n, say n+ε?

(Here, ε stands for epsilon, a microscopically small number).

The answer was very cleverly written using just two words:

n²+2 can.

Two figures are also attached with the paper, using which they have explained the same.

The problem is about how many equilateral triangles of side 1 unit can fit into a bigger equilateral triangle of ,say, n units.

We can see that that number is n².

For example, we see that an equilateral triangle of side 3 units can fit in 3²=9 equilateral triangles of side 1 unit.

This is an extension of the above problem, where the side length of the equilateral triangle is n+ε. Obviously, we need more than n² triangles to fit in here as the side length is greater than n.

So, the equilateral triangle’s side length has been split into two:

1.     n-1 and

2.    1+ε.

Both add up to make n+ε.

Using the previous formula, we can state that the number of triangles required to fill a triangle of side length n-1 is (n-1)². 

The number of triangles required to fill the trapezium with lower base equal to n+ε is n+1. Triangles have to be overlapped to get the same. The remaining area in the unfilled trapezium can be filled with n unit triangles. 

So, the total triangles required is:

 (n-1)² +n+1+n

=n²+1-2n+2n+1

=n²+2

Hence proved….

Hello Everyone!

Welcome to the blog on STEM (Science, Technology, Engineering and Mathematics) titled 'Three friends and a Byte of STEM'.
We will post interesting titbits about the vast, but interesting universe of STEM.